(修復 Delta_y) |
小无编辑摘要 |
||
| 第203行: | 第203行: | ||
* [https://pbs.twimg.com/media/DmCI89EV4AAwKVM.jpg:orig BM4 完整的評論] by koteitan (BM4 的閱讀和評論偽BASIC程序) |
* [https://pbs.twimg.com/media/DmCI89EV4AAwKVM.jpg:orig BM4 完整的評論] by koteitan (BM4 的閱讀和評論偽BASIC程序) |
||
| − | [[en:Bashicu matrix system |
+ | [[en:Bashicu matrix system]] |
| + | [[ja:バシク行列システム]] |
||
| + | [[fr:Système de matrice de Bashicu]] |
||
[[Category:Bashicu矩陣系統]] |
[[Category:Bashicu矩陣系統]] |
||
[[Category:記號]] |
[[Category:記號]] |
||
2021年10月17日 (日) 14:28的最新版本
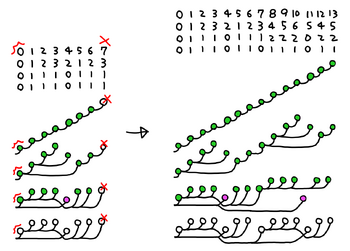
Bashicu矩陣系統的擴展實例
Bashicu矩陣系統 (Bashicu matrix system;BMS) 是一種生成 bashicu[1] 在2014年發明的巨大數字的算法[2]。
單行矩陣 (原始數列系統, Primitive Sequence System, PrSS) 具有 \(f_{\epsilon_0}(n)\) 強度。 雙行矩陣 (對數列系統, Pair Sequence System, PSS) 大於TREE(n),具有 \(f_{\psi(\Omega_{\omega})}(n)\) 強度。 3行矩陣(三重數列系統)大於SCG(n), n 行矩陣的增加率未知哪個序數對應。該函數被認為弱於Loader數的函數。
記法
Bashicu 矩陣 是一個矩陣,其元素是非負整數,如
- \(\begin{pmatrix} a_{11} & a_{12} & a_{13}\\ a_{21} & a_{22} & a_{23} \end{pmatrix}\)
通過排列像 \((a_{11},a_{21})(a_{12},a_{22})(a_{13},a_{23})\) 這樣的列向量的轉置矩陣來表示這是 Bashicu 矩陣的數列表示法。Bashicu 矩陣 \({\boldsymbol S}[n]\) 作從自然數 \(n\) 到自然數 \({\boldsymbol S}[n]\) 的函數起作用並並寫成 \((0,0)(1,1)(2,2)(3,3)(3,2)[n]\)。
定義
Bashicu 通過編程語言 BASIC 的偽語言使用 Bashicu 矩陣系統定義了Bashicu 矩陣數[3]。
由於 Bashicu 創建的程序並非用於執行,因此Fish創建了一個程序 “Bashicu 矩陣計算機”,顯示計算過程,該計劃由 Bashicu 驗證。因此, Bashicu 矩陣的形式定義在 Bashicu 矩陣計算機源代碼[4][5]中描述。
數學定義
如果您將 Bashicu 矩陣數作為公式編寫,它將如下所示[6]。
\begin{eqnarray*} \mathrm{Bashicu 矩陣數:}~K&=&\mathrm{Bm}^{10}(9)\\ \mathrm{大函數:}~\mathrm{Bm}(n)&=&\mathrm{expand}((\underbrace{0,0,\cdots,0}_{n+1})(\underbrace{1,1,\cdots,1}_{n+1})[n])\\ \mathrm{擴張規則:}~\mathrm{expand}([n])&=&n\\ \mathrm{expand}({\boldsymbol S}[n])&=&\left\{\begin{array}{ll} \mathrm{expand}({\boldsymbol S}_0\cdots{\boldsymbol S}_{X-2}[f(n)])&(\mathrm{if}~\forall y~S_{(X-1)y}=0)\\ \mathrm{expand}({\boldsymbol G}{\boldsymbol B}^{(0)}{\boldsymbol B}^{(1)}{\boldsymbol B}^{(2)} \cdots {\boldsymbol B}^{(f(n))}[f(n)])&(\mathrm{otherwise})\\ \end{array}\right.\\ \mathrm{激活函數:}~f(n)&=&n^2\\ \mathrm{矩陣:}~{\boldsymbol S}&=&{\boldsymbol S}_0{\boldsymbol S}_1\cdots{\boldsymbol S}_{X-1}\\ \mathrm{列:}~{\boldsymbol S}_x&=&(S_{x0},S_{x1},\cdots,S_{x(Y-1)})\\ \mathrm{好的部分:}~{\boldsymbol G}&=&{\boldsymbol S}_0{\boldsymbol S}_1\cdots{\boldsymbol S}_{r-1}\\ \mathrm{壞的部分:}~{\boldsymbol B}^{(a)}&=&{\boldsymbol B}_0^{(a)}{\boldsymbol B}_1^{(a)}\cdots{\boldsymbol B}_{X-2-r}^{(a)}\\ \mathrm{壞的部分的列:}~{\boldsymbol B}_x^{(a)}&=&(B_{x0}^{(a)},B_{x1}^{(a)},\cdots,B_{x(Y-1)}^{(a)})\\ \mathrm{壞的部分的元素:}~B_{xy}^{(a)}&=&S_{(r+x)y}+a\Delta_{y}A_{xy}\\ \mathrm{增加量:}~\Delta_{y}&=&\left\{\begin{array}{ll} S_{(X-1)y}-S_{ry}&(\mathrm{if}~y\lt t)\\ 0 &(\mathrm{if}~y\geq t) \end{array}\right.\\ \mathrm{增加矩陣:}~A_{xy}&=&\left\{\begin{array}{ll} 1 &(\mathrm{if}~ \exists a( r=(P_{y})^a(r+x)))\\ 0 &(\mathrm{否則}) \end{array}\right.\\ \mathrm{非零最下行:}~t&=&\max\{y|S_{(X-1)y}\gt 0\}\\ \mathrm{壞根:}~r &=& P_t(X-1)\\ S_{xy}~\mathrm{的親}:~P_{y}(x)&=&\left\{\begin{array}{ll} \max\{p|p\lt x \land S_{py} \lt S_{xy} \land \exists a( p=(P_{y-1})^a(x))\} & (\mathrm{if}~y\gt 0)\\ \max\{p|p\lt x \land S_{py} \lt S_{xy} \} & (\mathrm{if}~y=0)\\ \end{array}\right.\\ \end{eqnarray*}
計算示例
根據上述規則計算 \((0,0,0)(1,1,1)(2,2,2)(3,3,3)(4,2,0)[2]\) 。 \begin{eqnarray*}{\boldsymbol S} &=& {\boldsymbol S}_0{\boldsymbol S}_1{\boldsymbol S}_2{\boldsymbol S}_3{\boldsymbol S}_4\\ &=&(S_{00},S_{01},S_{02})(S_{10},S_{11},S_{12})(S_{20},S_{21},S_{22})(S_{30},S_{31},S_{32})(S_{40},S_{41},S_{42})\\ &=&(0,0,0)(1,1,1)(2,2,2)(3,3,3)(4,2,0) \end{eqnarray*}
- 第1行的親:最右邊的元素小於第1行的最右列 \(S_{40} = 4\) 左邊是 \(S_{30}=3\)。因此,小於第一行和左邊元素的最右邊元素稱為親。
\(S_{xy}\) 的親的列是 \(P_y(x)\) 。
- 直接祖先: 直接祖先的父母,或者你自己稱為那個元素的直接祖先。在這種情況下、\(S_{40} = 4\) 的直接祖先是 \(S_{40}=4,~S_{30}=3,~S_{20}=2,~S_{10}=1,~S_{00}=0\) 。
- 第二行和後續行的親: 第二行和後續行、對於給定的元素 \(S_{xy}\),與元素的直接祖先相同的序列 \((P_{y-1})^a(x)\) 高於該元素它在並且小於元素 \(S_{xy}\) 並且在左邊,最右邊的元素是親。
- 壞根: 最右列 \(X-1\) 的非零最下行 \(t\) 的親的列 \(P_t(X-1)\) 是 壞根 \(r\), 壞根將成為好的部分沒有復制 \({\boldsymbol G}\) 和壞部分複制 \({\boldsymbol B}^{(0)}\)的邊界。在這種情況下、第2行是非零最下行,壞根是第2行的最右列 \(S_{41} = 2\) 的親,換句話說,是\(S_{11}=1\),壞根是第2列 (\(r=1\))。
- 好的部分,壞的部分: 它變成\({\boldsymbol S}_r = (1,1,1)\) 並變成 \({\boldsymbol G} = (0,0,0), {\boldsymbol B}^{(0)} = (1,1,1)(2,2,2)(3,3,3)\) 。
- 增加量: 使用壞根 \({\boldsymbol S}_r = (1,1,1)\) 和修剪後的孩子的值 \({\boldsymbol S}_{X-1} = (4,2,0)\) 計算增加量為 \((\Delta_0, \Delta_1, \Delta_2) = (3,0,0)\)。
- 增加矩陣 是一個矩陣,其中壞根作為直接祖先的元素是1。在這種情況下、\(A_{xy}=(1,1,1)(1,1,1)(1,1,1)\) 。
- 壞部分複制: 由此壞部分 \({\boldsymbol B}^{(a)}\) 成 \({\boldsymbol B}^{(0)} = (1,1,1)(2,2,2)(3,3,3)\), \({\boldsymbol B}^{(1)} = (4,1,1)(5,2,2)(6,3,3)\), \({\boldsymbol B}^{(2)} = (7,1,1)(8,2,2)(9,3,3)\), \({\boldsymbol B}^{(3)} = (10,1,1)(11,2,2)(12,3,3)\), \({\boldsymbol B}^{(4)} = (13,1,1)(14,2,2)(15,3,3)\)。
- 由 擴張規則, \({\boldsymbol S}[2] = {\boldsymbol G}{\boldsymbol B}^{(0)}{\boldsymbol B}^{(1)}{\boldsymbol B}^{(2)}{\boldsymbol B}^{(3)}{\boldsymbol B}^{(4)}[4]\) 那是 (0,0,0)(1,1,1)(2,2,2)(3,3,3)(4,2,0)[2] = (0,0,0)(1,1,1)(2,2,2)(3,3,3)(4,1,1)(5,2,2)(6,3,3)(7,1,1)(8,2,2)(9,3,3)(10,1,1)(11,2,2)(12,3,3)(13,1,1)(14,2,2)(15,3,3)[4] 。如果以矩陣的形式表示,它將變為這樣。
\[\begin{pmatrix} 0 & 1 & 2 & 3 & 4\\ 0 & 1 & 2 & 3 & 2\\ 0 & 1 & 2 & 3 & 0\\ \end{pmatrix}[2] = \begin{pmatrix} 0 & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12 & 13 & 14 & 15\\ 0 & 1 & 2 & 3 & 1 & 2 & 3 & 1 & 2 & 3 & 1 & 2 & 3 & 1 & 2 & 3 \\ 0 & 1 & 2 & 3 & 1 & 2 & 3 & 1 & 2 & 3 & 1 & 2 & 3 & 1 & 2 & 3 \\ \end{pmatrix}[4]\]
這個結果與 Bashicu 矩陣計算機的計算結果 重合。
擴展的方法有點複雜,但已經表明通過用多行九頭蛇表[7]達它可以很容易地理解它。
起色
Hyp cos顯示了一個示例,其中計算未在2016年4月28日的英語版本的談話頁面上完成,與 Bashicu 於2015年8月21日定義的 Bashicu 矩陣(稱為BM1)的第一版相反。之後,Bashicu 在博客文章中發布了Bashicu Matrix矩陣2(BM2)作為Bashichu 數字的 BASIC 程序[8]。此外,Bashicu 創建了一個評論幻燈片[9]。
之後,在2018年6月12日,BM3由 Basicu 定義。[10]但、6月29日Alemagno12未顯示的示例顯示[11]。然後,2018年8月28日Bubby3 展示了一個BM2不會停止的例子[12]。
該定義最終由Basik在2018年9月1日更正,現在是 版本4。
此外,直到BM4出生,許多亞種如BM2.2, BM2.3, BM3.1, BM3.2 被提出[13][14]。
停機的證明
關於 Bashicu 矩陣的計算是否總是結束的問題尚未解決, 黑羽カフカ[15]概述了在某些條件下計算完成到2ch的「大量搜索線程的證據」[16]。但是,根據隨後的檢查,證據並不完整[17]。
在2018年11月11日P進大好きbot證明了對數列系統的停止性質,它將基礎矩陣限制為2行[18]。
評估尺寸
單行矩陣(原始數列系統)具有 \(f_{\epsilon_0}(n)\) 強度。
\begin{eqnarray*} ()&=&0\\ (0)&=&1\\ (0)(0)&=&2\\ (0)(0)(0)&=&3\\ (0)(1)&=&\omega\\ (0)(1)(0)&=&\omega+1\\ (0)(1)(0)(0)&=&\omega+2\\ (0)(1)(0)(0)(0)&=&\omega+3\\ (0)(1)(0)(1)&=&\omega2\\ (0)(1)(0)(1)(0)&=&\omega2+1\\ (0)(1)(0)(1)(0)(1)&=&\omega3\\ (0)(1)(0)(1)(0)(1)(0)(1)&=&\omega4\\ (0)(1)(1)&=&\omega^2\\ (0)(1)(1)(0)&=&\omega^2+1\\ (0)(1)(1)(0)(0)&=&\omega^2+2\\ (0)(1)(1)(0)(1)&=&\omega^2+\omega\\ (0)(1)(1)(0)(1)(0)&=&\omega^2+\omega+1\\ (0)(1)(1)(0)(1)(0)(1)&=&\omega^2+\omega2\\ (0)(1)(1)(0)(1)(1)&=&\omega^22\\ (0)(1)(1)(0)(1)(1)(0)(1)(1)&=&\omega^23\\ (0)(1)(1)(0)(1)(1)(0)(1)(1)(0)(1)(1)&=&\omega^24\\ (0)(1)(1)(1)&=&\omega^3\\ (0)(1)(1)(1)(1)&=&\omega^4\\ (0)(1)(1)(1)(1)(1)&=&\omega^5\\ (0)(1)(2)&=&\omega^\omega\\ (0)(1)(2)(0)&=&\omega^\omega+1\\ (0)(1)(2)(0)(0)&=&\omega^\omega+2\\ (0)(1)(2)(1)&=&\omega^{\omega+1}\\ (0)(1)(2)(1)[64]&\gt&\mathrm{葛立恒数}\\ (0)(1)(2)(0)(1)(2)&=&\omega^\omega2\\ (0)(1)(2)(0)(1)(2)(0)(1)(2)&=&\omega^\omega3\\ (0)(1)(2)(1)&=&\omega^\omega\omega=\omega^{\omega+1}\\ (0)(1)(2)(1)(0)(1)(2)(1)&=&\omega^\omega\omega=\omega^{\omega+1}2\\ (0)(1)(2)(1)(0)(1)(2)(1)(0)(1)(2)(1)&=&\omega^{\omega+1}3\\ (0)(1)(2)(1)(1)&=&\omega^{\omega+2}\\ (0)(1)(2)(1)(1)(1)&=&\omega^{\omega+3}\\ (0)(1)(2)(1)(1)(1)(1)&=&\omega^{\omega+4}\\ (0)(1)(2)(1)(2)&=&\omega^{\omega2}\\ (0)(1)(2)(1)(2)(1)(2)&=&\omega^{\omega3}\\ (0)(1)(2)(1)(2)(1)(2)(1)(2)&=&\omega^{\omega4}\\ (0)(1)(2)(2)&=&\omega^{\omega^2} \\ (0)(1)(2)(2)[n]&\gt& \underbrace{n\rightarrow n \rightarrow \cdots \rightarrow n}_{n \mathrm{个的} n} \\ (0)(1)(2)(2)(2)&=&\omega^{\omega^3}\\ (0)(1)(2)(2)(2)(2)&=&\omega^{\omega^4}\\ (0)(1)(2)(3)&=&\omega^{\omega^\omega}\\ (0)(1)(2)(3)(4)&=&\omega^{\omega^{\omega^\omega}}\\ (0)(1)(2)(3)(4)(5)&=&\omega^{\omega^{\omega^{\omega^\omega}}}\\ (0)(1)(2)(3)(4)(5)...&<&\epsilon_0 \end{eqnarray*}
以這種方式 可以容易地用\(\omega\) 表示原始數列和下一對數列。
雙行矩陣(對數列系統)具有 \(f_{\psi(\Omega_{\omega})}(n)\) 強度用 Buchholz 的 \(\psi\) 函數。
\begin{eqnarray*} (0,0)(1,1)&=&\epsilon_0\\ (0,0)(1,1)(2,1)&=&\zeta_0\\ (0,0)(1,1)(2,1)(2,1)&=&\eta_0\\ (0,0)(1,1)(2,1)(2,1)(2,1)&=&\varphi(4,0)\\ (0,0)(1,1)(2,1)(2,1)(2,1)(2,1)&=&\varphi(5,0)\\ (0,0)(1,1)(2,1)(3,0)&=&\varphi(\omega,0)\\ (0,0)(1,1)(2,1)(3,1)&=&\Gamma_0\\ &=&\varphi(1,0,0)\\ &=&\mathrm{(Feferman-Schutte~ordinal)} \end{eqnarray*} \begin{eqnarray*} (0,0)(1,1)(2,1)(3,1)(1,1)(2,1)(3,1)&=&\Gamma_1=\varphi(1,0,1)\\ (0,0)(1,1)(2,1)(3,1)(1,1)(2,1)(3,1)(1,1)(2,1)(3,1) &=&\Gamma_2=\varphi(1,0,2)\\ (0,0)(1,1)(2,1)(3,1)(3,0)&=&\Gamma_\omega=\varphi(1,0,\omega)\\ (0,0)(1,1)(2,1)(3,1)(1,0)(2,1)(3,1)(4,1)&=&\Gamma_{\Gamma_0}=\varphi(1,0,\varphi(1,0,0))\\ (0,0)(1,1)(2,1)(3,1)(2,1)&=&\Gamma_{\Gamma_{\Gamma_\vdots}}\\ &=&\varphi(1,1,0)\\ (0,0)(1,1)(2,1)(3,1)(2,1)(3,1)&=&\varphi(2,0,0)\\ (0,0)(1,1)(2,1)(3,1)(2,1)(3,1)(2,1)(3,1)&=&\varphi(3,0,0)\\ (0,0)(1,1)(2,1)(3,1)(2,1)(3,1)(2,1)(3,1)(2,1)(3,1)&=&\varphi(4,0,0)\\ (0,0)(1,1)(2,1)(3,1)(3,0)&=&\varphi(\omega,0,0)\\ (0,0)(1,1)(2,1)(3,1)(3,0)(4,1)(5,1)(6,1)&=&\varphi(\varphi(1,0,0),0,0)\\ (0,0)(1,1)(2,1)(3,1)(3,0)(4,1)(5,1)(6,1)(6,0)(7,1)(8,1)(9,1)&=&\varphi(\varphi(\varphi(1,0,0),0,0),0,0) \end{eqnarray*} \begin{eqnarray*} (0,0)(1,1)(2,1)(3,1)(3,1)&=&\varphi(1,0,0,0)\\ &=&\varphi(\varphi(\varphi(\cdots,0,0),0,0),0,0)\\ (0,0)(1,1)(2,1)(3,1)(3,1)(3,1)&=&\varphi(1,0,0,0,0)\\ (0,0)(1,1)(2,1)(3,1)(3,1)(3,1)(3,1)&=&\varphi(1,0,0,0,0,0)\\ (0,0)(1,1)(2,1)(3,1)(4,0)&=&\varphi(1,0,0,\cdots,0)\\ &=&\psi(\Omega^{\Omega^\omega})\\ &=&\mathrm{Small~Veblen~Ordinal} \end{eqnarray*}
從這裡開始,我不能用 Veblen 函數寫,Bashicu 矩陣功能強大,很難通過快速增加的函數分析3行矩陣(三重數列系統)的增加速度,所以有很多模棱兩可的分析用定義失敗的ψ函數。 (0,0,0)(1,1,1) 以上基于 Username5243 的模棱兩可的分析用定義失敗的ψ函數[19]。在此之後,看看黑色羽毛的分析[20][21][22][23][24][25]用Rathjen的ψ函數。
源
- ↑ 作者:Bashicu
- ↑ Bashicu 矩陣計算機
- ↑ BASIC語言的大數概要
- ↑ Bashicu 矩陣計算機源代碼
- ↑ Bashicu 矩陣的C語言定義
- ↑ Bashicu 矩陣的數學定義
- ↑ 忽略上面模型的九頭蛇圖
- ↑ BASIC語言中的大量數字摘要
- ↑ Bashicu 矩陣系統的解釋
- ↑ Bashicu 矩陣版本3
- ↑ 不停止BM3的示例
- ↑ 不停止BM2的示例
- ↑ Bashicu 矩陣的變體規則的分類
- ↑ 所有BMS版本及其差異的列表
- ↑ User:KurohaKafka
- ↑ 巨大数探索スレッド11.75: 152-155 和 copy
- ↑ Bashicu矩陣的可計算性證明(評論字段參考)
- ↑ 對數列系統的停機證明
- ↑ BM4 Analysis by Username5243
- ↑ 黑羽カフカ的分析
- ↑ Bashicu的分析
- ↑ 黑羽カフカ的分析
- ↑ Matthew 的分析
- ↑ Aarex 的分析
- ↑ Bashicu 矩陣分析的鏈接 by koteitan
相關鏈接
- Bashicu 矩陣系統的解釋 by Bashicu
- Bashicu Matrix Calculator by Fish
- Hydra Viewer by koteitan (這顯示了使用 hydra 計算對數列)
- BM4 完整的評論 by koteitan (BM4 的閱讀和評論偽BASIC程序)
