| クサイ関数 | |
|---|---|
| 型 | 計算不可能
|
クサイ関数 (xi function) は、Adam P. Goucher が定義した計算不可能な関数であり、SKIコンビネータ計算の一種に基づいている[1]。クサイ関数はビジービーバー関数よりも増加速度が大きい。Aarex Tiaokhiao はクサイ関数の無邪気な拡張としてAarex関数を定義した。
Goucher は「ラヨ関数が急増加関数では \(\omega_\omega^\text{CK}\) 相当であり、クサイ関数は更に増大度が早く急増加関数では 写像 \(\alpha \mapsto \omega_\alpha^\text{CK}\)の最小の不動点相当であり、これまでに定義されたいかなる関数よりも増加速度が速い」と証明なく主張した[1]が、Goucherが主張する「急増加関数階層における \(\omega_{\alpha}^{\text{CK}}\)」はほぼ全て「\(\alpha\)階オラクルチューリングマシンで計算でき、それより弱い計算モデルでは計算する方法が分からない関数」程度の意味しかなく、実際の急増加関数との比較は全く行われていない。解析の根拠はなく、そもそも基本列すら定めておらず、基本列をある程度自然に定めたとしてもラヨ関数の評価は完全に誤っている。
定義[]
SKIコンビネータ計算は、コンビネータと呼ばれる3つの記号 S, K, I を使う。ベータ簡約と言われるプロセスによって、一番左の演算子が取り除かれ、次のいずれかの演算を実行する。
- \(I(x) = x\)
- \(K(x, y) = x\)
- \(S(x, y, z) = x(z, y(z))\)
たとえば、S(K, S, K(I, S)) にベータ簡約を繰り返すと K(K(I, S), S(K(I, S))) = K(I, S) = I となる。SKI式の中には、ベータ簡約によって最終的にIになるものもあり、I以外の短い式になるものもあり、無限に増加を続けるものもある。SKI式をベータ簡約することによって、最終的にn個のコンビネータの式になるとき、出力のサイズがnであるとする。
SKI式そのものはチューリングマシンよりも強くない。しかし、そこに次のように神託コンビネータ\(Ω\)を加えることで、著しく強くすることができる。
- \(Ω(x, y, z)\); \(x\) の最終的なベータ簡約結果が \(I\)になるならば\(y\)、そうでない場合は \(z\) が出力される。
n個の記号からなる式からベータ簡約をはじめたて、最終的に得られる最大の有限の出力を Ξ(n) とする。ゲーデルの不完全性定理により、SKIΩ計算式は矛盾を含んでいる可能性があるが、そのような式は Ξ の計算では無視される。
さらにもう一つの神託コンビネータ Ω’ を加えることができる。これは Ω と同様に働くが、SKIΩ 式が矛盾を含んでいないか(パラドックスを生じないか)をチェックすることができる。この新しいコンビネータを使うことで、Ξ の異なるバージョンである Ξ2 を作ることができ、通常のクサイ関数よりもさらに増加速度が大きくなる。
値[]
いくつかの確定した値と下限値を下に示す。
\begin{eqnarray} \Xi(1) &=& 1 \\ \Xi(2) &=& 2 \\ \Xi(3) &=& 3 \\ \Xi(4) &=& 4 \\ \Xi(5) &=& 6 \\ \Xi(6) &=& 17 \\ \Xi(7) &=& 51 \\ \Xi(8) &\geq& 137 \\ \Xi(9) &\geq& 519 \\ \Xi(10) &\geq& 1041 \\ \Xi(11) &\geq& 2085 \\ \Xi(12) &\geq& 4173 \\ \Xi(16) &\geq& 2^{2^9}+1 > f_3(2) \\ \Xi(21) &>& f_4(2) \\ \Xi(25) &>& f_{\omega+1}(2) \\ \Xi(30) &>& f_{\omega+2}(2) > G\\ \Xi(38) &>& f_{\omega^2+1}(2) \\ \Xi(56) &>& f_{\omega^\omega+1}(2) \\ \Xi(117) &>& f_{\omega^{\omega^\omega}+1}(2) \\ \Xi(n) &>& 7F_{n-2} \text{ (for } n\geq 7) \\ \end{eqnarray}
ここで、 \(F_{n-2}\) はn-2番目の Fibonacci sequenceである。
勝利手順[]
下は\(\Xi(n)\)に対するベータ簡約の一覧である。
\(\Xi(1),\Xi(2),\Xi(3)\) そして \(\Xi(4)\) においてはこの手順はつまらないものである。 それぞれ、 S, S(S), S(SS) , S(SSS) である。 \(5 \leq n \leq 7\) については、 次のようになる。
\(\Xi(5)\)[]
SSS(SI) S(SI)(S(SI))
\(\Xi(6)\)[]
SSS(SI)S S(SI)(S(SI))S SIS(S(SI)S) I(S(SI)S)(S(S(SI)S)) S(SI)S(S(S(SI)S)) SI(S(S(SI)S))(S(S(S(SI)S))) I(S(S(S(SI)S)))(S(S(SI)S)(S(S(S(SI)S)))) S(S(S(SI)S))(S(S(SI)S)(S(S(S(SI)S))))
\(\Xi(7)\)[]
\(\Xi(7)\) では初めて神託コンビネータが通常のSKIコンビネータを上回ることとなる。
SSS(SI)SΩ S(SI)(S(SI))SΩ SIS(S(SI)S)Ω I(S(SI)S)(S(S(SI)S))Ω S(SI)S(S(S(SI)S))Ω SI(S(S(SI)S))(S(S(S(SI)S)))Ω I(S(S(S(SI)S)))(S(S(SI)S)(S(S(S(SI)S))))Ω S(S(S(SI)S))(S(S(SI)S)(S(S(S(SI)S))))Ω S(S(SI)S)Ω((S(S(SI)S)(S(S(S(SI)S))))Ω) S(SI)S((S(S(SI)S)(S(S(S(SI)S))))Ω)(Ω((S(S(SI)S)(S(S(S(SI)S))))Ω)) SI((S(S(SI)S)(S(S(S(SI)S))))Ω)(S((S(S(SI)S)(S(S(S(SI)S))))Ω))(Ω((S(S(SI)S)(S(S(S(SI)S))))Ω)) I(S((S(S(SI)S)(S(S(S(SI)S))))Ω))(((S(S(SI)S)(S(S(S(SI)S))))Ω)(S((S(S(SI)S)(S(S(S(SI)S))))Ω)))(Ω((S(S(SI)S)(S(S(S(SI)S))))Ω)) S((S(S(SI)S)(S(S(S(SI)S))))Ω)(((S(S(SI)S)(S(S(S(SI)S))))Ω)(S((S(S(SI)S)(S(S(S(SI)S))))Ω)))(Ω((S(S(SI)S)(S(S(S(SI)S))))Ω)) S(S(SI)S)(S(S(S(SI)S)))Ω(Ω((S(S(SI)S)(S(S(S(SI)S))))Ω))(((S(S(SI)S)(S(S(S(SI)S))))Ω)(S((S(S(SI)S)(S(S(S(SI)S))))Ω)))(Ω((S(S(SI)S)(S(S(S(SI)S))))Ω))) S(SI)SΩ((S(S(S(SI)S)))Ω)(Ω((S(S(SI)S)(S(S(S(SI)S))))Ω))(((S(S(SI)S)(S(S(S(SI)S))))Ω)(S((S(S(SI)S)(S(S(S(SI)S))))Ω)))(Ω((S(S(SI)S)(S(S(S(SI)S))))Ω))) SIΩ(S(Ω))((S(S(S(SI)S)))Ω)(Ω((S(S(SI)S)(S(S(S(SI)S))))Ω))(((S(S(SI)S)(S(S(S(SI)S))))Ω)(S((S(S(SI)S)(S(S(S(SI)S))))Ω)))(Ω((S(S(SI)S)(S(S(S(SI)S))))Ω))) I(S(Ω))(Ω(S(Ω)))((S(S(S(SI)S)))Ω)(Ω((S(S(SI)S)(S(S(S(SI)S))))Ω))(((S(S(SI)S)(S(S(S(SI)S))))Ω)(S((S(S(SI)S)(S(S(S(SI)S))))Ω)))(Ω((S(S(SI)S)(S(S(S(SI)S))))Ω))) SΩ(Ω(S(Ω)))((S(S(S(SI)S)))Ω)(Ω((S(S(SI)S)(S(S(S(SI)S))))Ω))(((S(S(SI)S)(S(S(S(SI)S))))Ω)(S((S(S(SI)S)(S(S(S(SI)S))))Ω)))(Ω((S(S(SI)S)(S(S(S(SI)S))))Ω))) Ω((S(S(S(SI)S)))Ω)((Ω(S(Ω)))((S(S(S(SI)S)))Ω))(Ω((S(S(SI)S)(S(S(S(SI)S))))Ω))((((S(S(SI)S)(S(S(S(SI)S))))Ω)(S((S(S(SI)S)(S(S(S(SI)S))))Ω)))(Ω((S(S(SI)S)(S(S(S(SI)S))))Ω))) Ω((S(S(SI)S)(S(S(S(SI)S))))Ω)((((S(S(SI)S)(S(S(S(SI)S))))Ω)(S((S(S(SI)S)(S(S(S(SI)S))))Ω)))(Ω((S(S(SI)S)(S(S(S(SI)S))))Ω)))
\(\Xi(8)\) 以上[]
現在の\(\Xi(8)\) のコンビネータ候補は SSK(S(SSΩ))S である。
現在の \(\Xi(9)\) のコンビネータ候補は SSI((S(SS)S)S)K である。
現在の \(\Xi(10)\) のコンビネータ候補は SSI((S(SS)S)S)KS である。
現在の \(\Xi(11)\) のコンビネータ候補は SSI((S(SS)S)S)KKS である。
現在の \(\Xi(12)\) のコンビネータ候補は SSI((S(SS)S)S)KKKS である。
樹形図[]
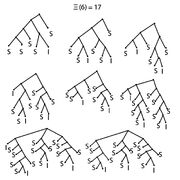
XI(6)の樹形図
コンビネータは樹形図を用いても表す事ができる。関数は左に、引数は右に示される。
出典[]
- ↑ 1.0 1.1 Goucher, Adam P. The Ξ function. Retrieved 14.03.2013.
