Séquence primitif

Le système de séquence primitif est un système de création de grands nombres créé par un utilisateur japonais du Wiki Googologie, Bashicu. Le nombre créé avec le système est appelé le nombre de la séquence primitif. Il a été posté sur le fil de discussion du grand nombre de 2channel comme le programme (message n°109) et ses exemples (n°135-140). C'est comme les vers de Beklemishev et sa force est de $f_{\varepsilon_0}(n)$. La taille du nombre de la séquence primitif est d'environ $f_{\varepsilon_0+1}(10)$.

Le système de séquence de la paire, qui est l'expansion du système de séquence primitif en deux rangées par Bashicu, a une force approchée de $f_{\psi(\Omega_{\omega})}(n)$ par rapport à la fonction de Buchholz. L'expansion en trois rangs par Bashicu est appelée système de séquence Trio. Leur généralisation par Bashicu s'appelle le système de matrice de Bashicu. Il comporte n rangs. Leur étude est actuellement en cours.

Le système de séquence hyper primitif, qui est une extension du système de séquence primitif utilisant le système de séquence de différence par un utilisateur japonais de Wiki Googologie Yukito a la force de $f_{\psi(\Omega_{\omega})}(n)$ par rapport à la fonction de Buchholz.

Définition

Définition originale par Basic

La première définition du nombre de séquences primitif a été publiée sur le site de communication 2channel sous forme de pseudo-code en langage Basic. Après cela, les définitions sont maintenues sur l'article dans le blog des utilisateurs de Wikia.

Définition mathématique

Bien que la définition originale soit écrite dans le pseudo-code du langage Basic, elle peut être décrite dans la définition mathématique suivante :

La séquence primitive est une liste d'entiers non négatifs S = (S₀, S₁, ..., S_k). La séquence primitive a le comportement de la fonction d'un entier non négatif n en un entier non négatif, la valeur de S[n] est définie comme suit :

• ()[n] = n.
• La bonne partie g et la mauvaise partie b de la séquence primitive sont définies comme suit : (r est le plus grand entier non négatif qui donne r<k and S_r<S_k dans la suite).
  • Lorsque r existe, que g et b soient g = (S₀,...,S_r-1), b = (S_r,...,S_k-1).
  • Lorsque r n'existe pas, soyons g = (S₀, ..., S_k-1), b=().
• Soit S[n], $S[n] = (g \frown b \underbrace{\frown b \frown \cdots \frown b}_{f(n) \mathrm{'s}~\frown b})[f(n)]$. Où, f(n) est f(n) = n².

$\frown$ est la concaténation de la séquence, par exemple, (0, 3, 2) $\frown$ (1, 4, 5) = (0, 3, 2, 1, 4, 5). P¹⁰(9) (P(n)=(0,...,n)[n]) est défini comme le numéro de séquence primitive avec le système de séquence primitive ci-dessus.

C'est la définition calquée sur le vers de Beklemishev. Notez que la position qui fait la division de g et b est différente de celle des vers de Beklemishev.

Explication de la définition

L'explication facile pour trouver r est la suivante : en cherchant le nombre S_k-1 du côté droit de la séquence, on trouve l'indice de l'un comme r. Par exemple, dans le cas de $(0, 1, 2, 3, 3, 1, 2, 3, 2, 3, 2, \underbrace{2}_{=S_k})[2]$, le nombre le plus à droite S_k est 2, cherchez 1 vers le côté gauche à partir de là, le premier 1 trouvé est S₅=1 donc r=5. Dans ce cas, b et g deviennent $(\underbrace{0, 1, 2, 3, 3}_{=g}, \underbrace{1, 2, 3, 2, 3, 2}_{=b}, 2)[2]$. Le support est [2] et f(n)=n², ils donnent

$\begin{array}{rl} S[2]&=&g\frown b~\underbrace{\frown b\frown b\frown b\frown b}_{2^2~\text{'s}}\\ &=&(\underbrace{0, 1, 2, 3, 3}_{=g}, \underbrace{1, 2, 3, 2, 3, 2}_{=b}, \underbrace{1, 2, 3, 2, 3, 2}_{=b}, \underbrace{1, 2, 3, 2, 3, 2}_{=b}, \underbrace{1, 2, 3, 2, 3, 2}_{=b}, \underbrace{1, 2, 3, 2, 3, 2}_{=b})[4]. \end{array}$

Cette S_r est souvent appelée bad root (mauvaise racine).

Calcul

La séquence primitive s'écrit souvent sous la forme S = (S₀ S₁ ... S_k) = (S₀)(S₁) .... (S_k) comme le cas particulier du système de matrice de Bashicu.

Le calcul du système de séquences primitives peut être effectué avec la Bashicu Matrix Calculator. Par exemple, le résultat du calcul de (0)(1)(2)(3)[2] devient comme ceci. (Elle croît si vous donnez la plus grande 'maximum length'.) Bien qu'elle semble continuer à croître, cette séquence atteint toujours la séquence vide à la fin et laisse [n]. Le calcul s'arrête alors après la sortie de [n]=n. Si vous donnez (0)(1)(2)[2] avec f(n)=n, vous pouvez voir le processus jusqu'à la fin.

En plus de cela, il peut être modifié pour correspondre à la hiérarchie de Hardy et il peut calculer $H_{\omega^\omega}(2) = 8$ like this.

Si l'on considère la fonction P(n) = (0,1,2, ..., n)[n], le taux de croissance de P(n) est d'environ $f_{\varepsilon_0}(n)$. Le nombre de séquence primitif est P¹⁰(9) et sa taille est $f_{\varepsilon_0+1}(10)$.

Correspondance avec l'ordinal

Chaque séquence primitive correspond à un ordinal inférieur à $\epsilon_0$. Les ordinaux correspondants sont toujours réduits dans le calcul des séquences primitives. Puisqu'il n'existe pas de chaîne descendante infinie d'ordinaux, le calcul des séquences primitives atteint nécessairement une fin.

Il existe un programme qui affiche les ordinaux correspondant aux séquences primitives La correspondance inverse des ordinaux aux séquences primitives de forme standard est démontrée de la manière suivante :

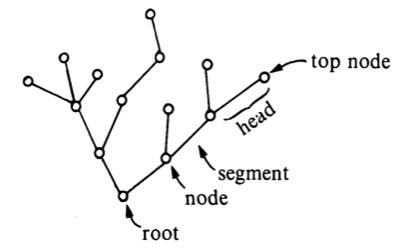
1. Ecrivez l'arbre d'hydre correspondant à un ordinal α donné. La figure ci-dessus représente $\omega^{\omega^\omega+\omega^3}+\omega^{\omega^2+1}$ comme l'article de Kirby et Paris (1982).
2. Commencez ci-dessous à partir du nœud racine (root node).
3. Ajoutez un nouvel élément 0 dans le dernier de la séquence lorsque vous montez en 1 ci-dessus à partir du nœud racine.
4. Ajoutez un nouvel élément "(le dernier élément) + 1" dans le dernier de la séquence lorsque vous montez en 1 au-dessus de l'autre nœud.
5. Lorsque vous atteignez l'extrémité de la branche et que vous descendez jusqu'au nœud de bifurcation (ancêtre commun) et que vous passez à une autre branche, ajoutez "(l'élément de bifurcation) + 1".
6. de sorte que le nombre dans le nœud devienne la valeur "(hauteur)-1".
7. Voici l'exemple pour correspondre à la figure comme ceci. La partie de $\omega^{\omega^{\omega}}$ est représentée par (0,1,2,3). Après cela, descendez de 3 noeuds, allez à la prochaine branche (segment), obtenez (1,2,2,2), il est ajouté dans la séquence. Après cela, (0,1,2,2,1) est ajouté de la même manière. Finalement, l'arbre d'hydre correspond à la séquence primitif (0,1,2,3,1,2,2,2,0,1,2,2,1).
8. $\omega^{\omega^\omega+\omega^3}+\omega^{\omega^2+1} = (0,1,2,3,1,2,2,2,0,1,2,2,1)$.

Voici des exemples de correspondance entre des ordinaux inférieurs à $\varepsilon_0$ et des séquences primitives de forme standard.

$\begin{array}{rl} 1 &=& (0) \\ 2 &=& (0,0) \\ 3 &=& (0,0,0) \\ \omega &=& (0,1) \\ \omega+2 &=& (0,1,0,0) \\ \omega \cdot 2 &=& (0,1,0,1) \\ \omega^2 &=& (0,1,1) \\ \omega^2+\omega &=& (0,1,1,0,1) \\ \omega^3 &=& (0,1,1,1) \\ \omega^\omega &=& (0,1,2) \\ \omega^{\omega^\omega} &=& (0,1,2,3) \\ \omega^{\omega^{\omega^\omega}} &=& (0,1,2,3,4) \\ \omega^{\omega^{(\omega^\omega+1)}} &=& (0,1,2,3,4,2) \\ \omega^{\omega^{\omega^{\omega^\omega}}} &=& (0,1,2,3,4,5) \\ \end{array}$

Programmes

Le code le plus court

Le code python qui exécute le système de séquence primitive est montré dans le site The Py_1 Function, qui est le JAM en ligne pour faire le grand nombre avec des codes courts.

Le code est de 72 octets et il calcule (0)(1)(2)(3)(4)(5)(6)(7)(8)(9)[9] en \(f(n)=n^2\).

x,*m=range(9,-1,-1)
while m:
   q,*m=m;x*=x
   if q:m=m[:m.index(q-1)+1]*x+m

Calculateurs d'expansion

• en C par fish: Bashicu matrix calculator
• en Javascript par koteitan: yaBMS
• en Javascript par koteitan: prss.html (See also a blog post with detailed explanations in Japanese or its English translation.)

Convertisseur ordinal

• en Python 2 par fish: Primitive sequence analyzer 原始数列解析 (See also a blog post with detailed explanations in Japanese.)
• en Javascript par koteitan: p2o

Convertisseurs de notation Hydra

• en Javascript par koteitan: hydraviewer(for Pair sequence system)
• en Javascript par naruyoko: BMS Hydra viewer(Multi-row supported)